처음 풀어보는 백준의 플래티넘 문제.
내가 풀었던 방식 부터 적을 생각이다.
우선 문제는 이름 그대로 최단 경로가 아닌 거의 최단 경로를 찾는다.
그래프에서 최단경로들의 간선을 제외한 그다음에 나오는 최단경로를 찾는 문제
우선 생각했던 방법은 다익스트라로 간선들을 지우면서 나간뒤 다익스트라를 한번더 돌릴예정이였다.
그렇게 테스트 하였지만 결과는 8% 실패
실패 이유는 다익스트라로 간선을 지울경우 간선이 하나만 지워지는 문제가 생긴다.
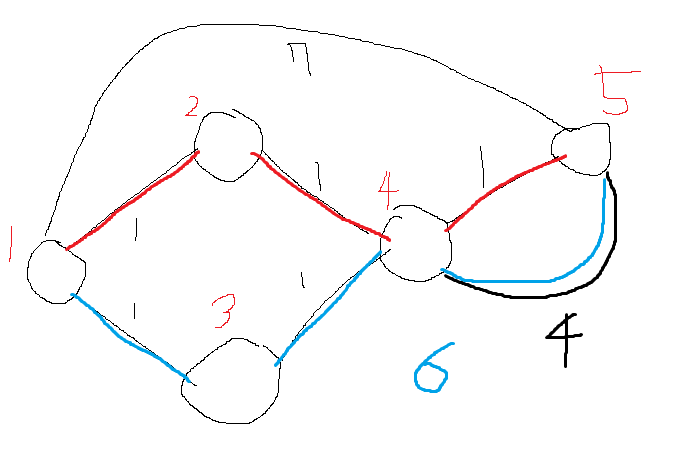
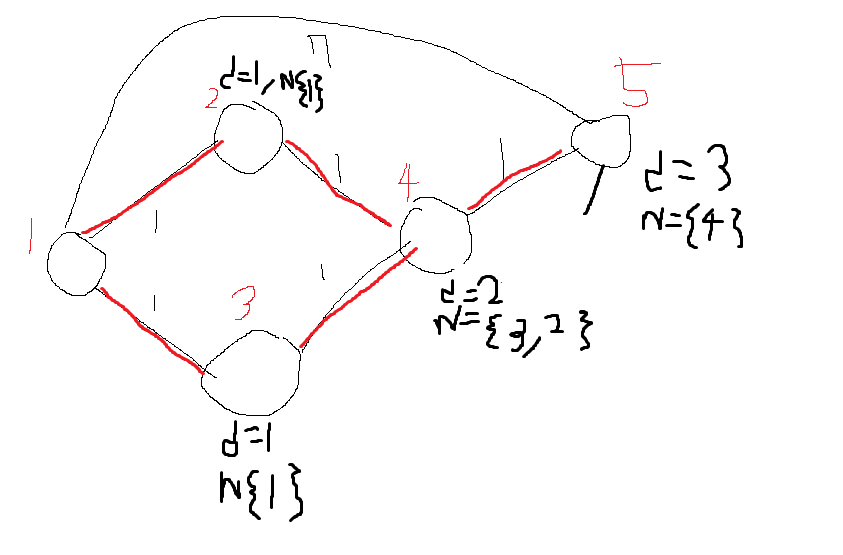
위 의경우 최단경로는 두개로 1 2 4 5 와 1 3 4 5가 있다.
거의 최단경로는 저두개를 제외한 1 ->5인 이여야 하지만
경로를 먼저 지워주게 될경우 4->5가 공유되지않으면서
거의최단경로는 6이 나오게된다.
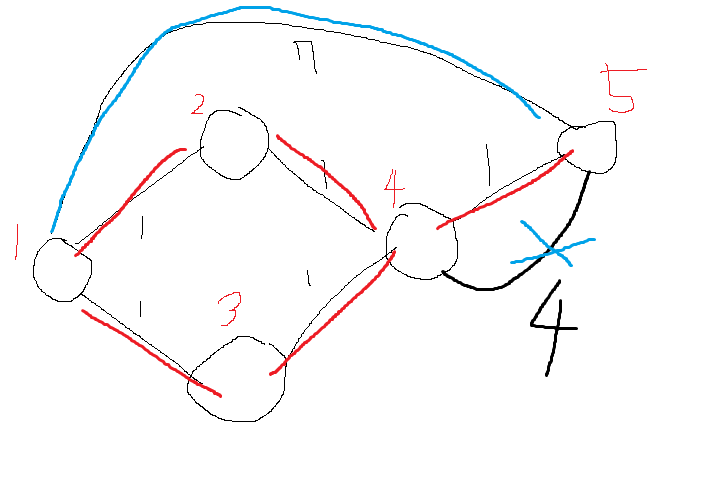
정상적인경우 위처럼 최단경로들을 제외하여 4->5로가는 길을 쓸수없기에 7이 나오지 못한다.
두번째 아이디어는 지나가면서 모든 지나온 간선 1->2 일경우 tuple<1,2> 식으로 queue 에 담아간뒤
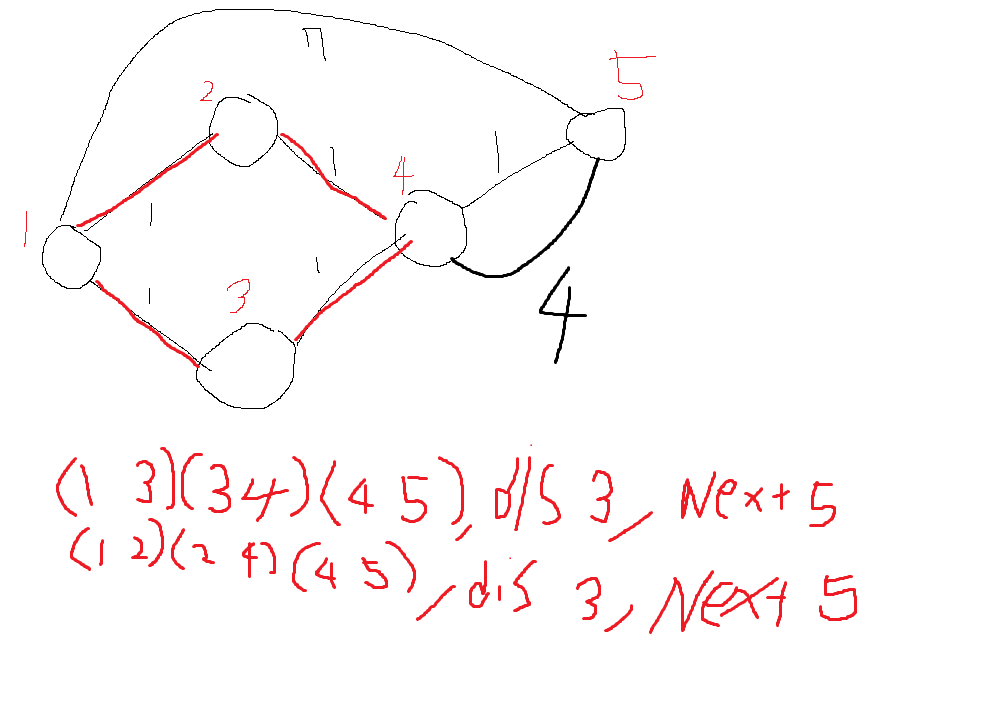
마지막 칸에 도착하였을경우 최적해로 도착한 queue내부의 간선중 지워지지 않은 간선을 지워주었다.
문제에서 실패는 없었지만 25%에서 메모리 초과가 났다.
여기서 한동안 고민을 하다. 문제를 알아냈다.
문제는 메모리 초과
queue로 간선을 담으면서 갈경우 특정 노드에서 만나는경우 왔던 간선을 유지하기위해
최단거리가 두개가 같은노드에서 만나면 둘다 큐에 넣어주었다.
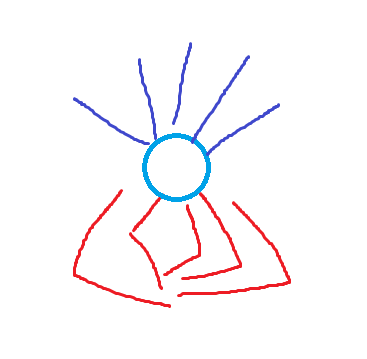
위 같이 이런경우 같은 노드에 만나는 경우 이후 노드의 값만큼 의미없는 계산이 기하급수적으로 늘어날수 있다.
이후 계산은 전부 똑같지만 일전의 계산때문에 그전 간선이 다른 만큼 계산이 늘어남
문제를 해결하기위해 코드를 크게 변경해주었다.
우선 다익스트라를 돌며 같은 중간노드에서 같은 값이 있을경우 를 해결하기위해
다익스트라에서 현재위치의 크기를 알아야 한다.
그뒤 현재 노드로 온 그전 노드의 위치를 알수있어야 한다.
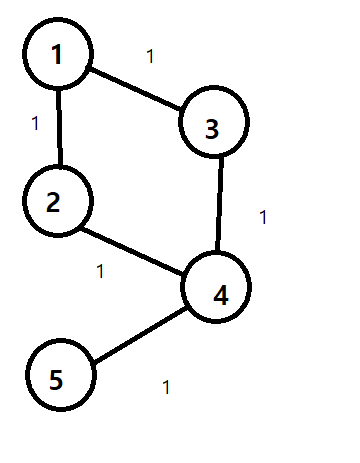
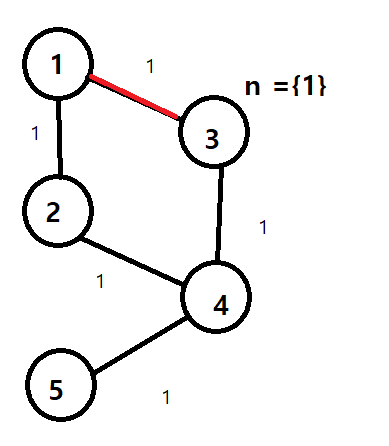
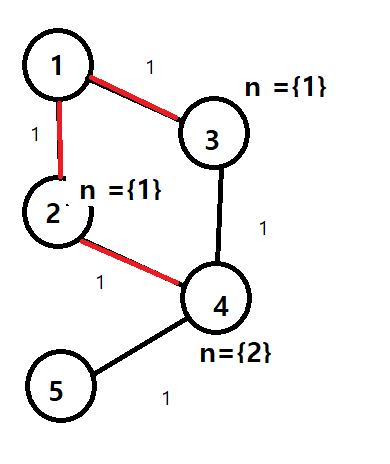
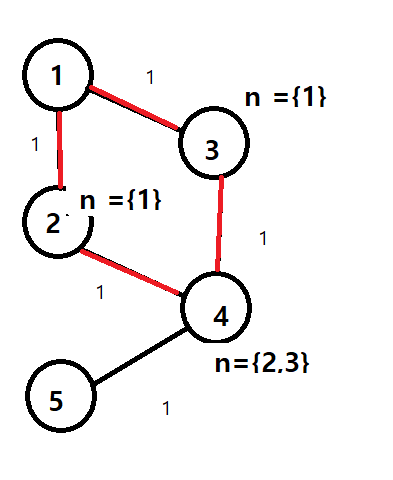
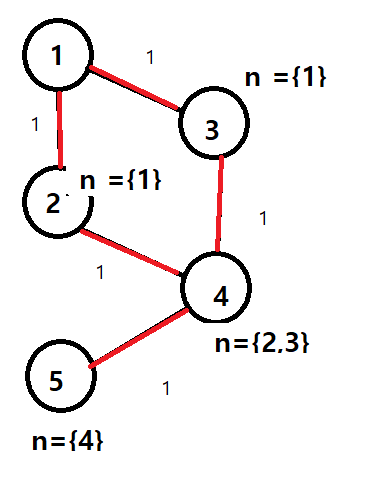
이렇게 만든경우
최소 큐 에서 더큰 같은 크기의 거리에서 만난 경우 그냥 그 위치에 왔던 노드를 표시해준다면
도착한뒤 돌아가면서 간선 제거를 해준다면
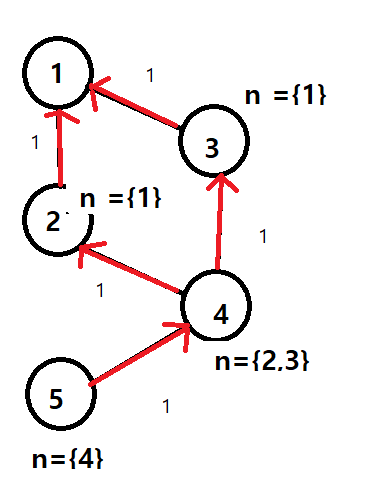
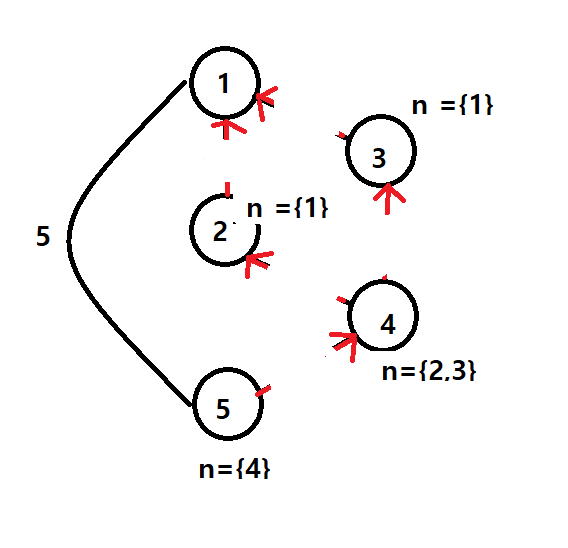
위 이미지 처럼
다익 두번 과 간선 지우는 bfs한번만에 해결가능하다.
아래는 해결코드다.
#include<queue>
#include <unordered_map>
#include<vector>
#include<iostream>
using namespace std;
#define cost 0
#define Nextroad 1
// 매직넘버
#define MM_Num 9999999
const auto& mt = make_tuple(MM_Num, MM_Num);
//간선을 확인하며 삭제하는 함수
void Distory(unordered_map<int, vector<tuple<int, int>>>& Umap, vector< queue<int>>& nodeGansun, int end) {
//도착지점에서 돌아가면서 왔던길 삭제
while (!nodeGansun[end].empty())
{
int num = nodeGansun[end].front();
nodeGansun[end].pop();
for (auto& um : Umap[num]) {
if (get<1>(um) == end) {
um = make_tuple(MM_Num, MM_Num);
Distory(Umap, nodeGansun, num);
}
}
}
}
//간선을 기록하며 가는 다익스트라
void find_FIRST_DS(unordered_map<int, vector<tuple<int, int>>>& Umap, int start, int end, int nodesize) {
priority_queue<tuple<int, int, int>> nextxy;
vector<int> noodBool(nodesize + 1, MM_Num);
vector< queue<int>>nodeGansun(nodesize + 1, queue<int>());
noodBool[start] = MM_Num;
tuple<int, int, int> nxy;
int d = 0, arrowRoad = 0, arrowcost = 0;
nextxy.emplace(make_tuple(0, start, start));
int first = MM_Num;
while (!nextxy.empty())
{
nxy = nextxy.top();
nextxy.pop();
arrowcost = -get<0>(nxy);
arrowRoad = get<1>(nxy);
if (get<1>(nxy) == end) {
if (first == get<0>(nxy)) {
first = get<0>(nxy);
break;
}
}
//최단거리 이며 다른 간선을 통해 하나의 노드에 도착했을경우
// 이전의 노드 를 현재 노드에 저장
if (noodBool[arrowRoad] == MM_Num || noodBool[arrowRoad] > (arrowcost)) {
noodBool[arrowRoad] = arrowcost;
nodeGansun[arrowRoad] = queue<int>();
nodeGansun[arrowRoad].push(get<2>(nxy));
}
else if (noodBool[arrowRoad] == (arrowcost))
{
nodeGansun[arrowRoad].push(get<2>(nxy));
continue;
}
else continue;
d = get<0>(nxy);
for (int i = 0; i < Umap[get<Nextroad>(nxy)].size(); ++i) {
tuple<int, int> arrow = Umap[get<1>(nxy)][i];
arrowRoad = get<1>(arrow);
arrowcost = get<0>(arrow);
if (noodBool[arrowRoad] == MM_Num || noodBool[arrowRoad] > (arrowcost + -(d))) {
nextxy.emplace(make_tuple(-(arrowcost + -(d)), get<1>(arrow), get<1>(nxy)));
}
}
}
while (!nextxy.empty()) {
auto b = nextxy.top();
nextxy.pop();
if (get<1>(b) == end && get<0>(b) == first) {
nodeGansun[end].push(get<2>(b));
}
}
Distory(Umap, nodeGansun, end);
return;
}
//그냥 다익스트라
int find_second_DS(unordered_map<int, vector<tuple<int, int>>>& Umap, int start, int end, int nodesize) {
priority_queue<tuple< int, int>> nextxy;
vector<bool> noodBool(nodesize + 1, false);
tuple<int, int> nxy;
nextxy.emplace(make_tuple(0, start));
bool lastnode = false;
noodBool[start] = true;
//다음 갈 장소가 없으면 끝냄
while (!nextxy.empty())
{
nxy = nextxy.top();
nextxy.pop();
온길 기록
noodBool[get<1>(nxy)] = true;
//도착지에 도착하면 최단거리 리턴
if (get<1>(nxy) == end) {
return (-get<0>(nxy));
}
for (const auto& arrow : (Umap[get<1>(nxy)])) {
//현재 간선에서 갈수있는 간선들 이동
//만약 지워진 간선일경우
if (get<1>(arrow) == MM_Num)continue;
// 이미 왔던 간선일경우
if (noodBool[get<1>(arrow)]) {
continue;
}
// 다음간선 + 이동값 queue 추가
nextxy.emplace(make_tuple(-(get<0>(arrow) + -(get<0>(nxy))), get<1>(arrow)));
}
}
return (-1);
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
cin.tie(NULL);
int NodeSize = 0, NodeLoadSize = 0, Start = 0, end = 0;
int node = 0, Xnode = 0, Dis = 0;
unordered_map<int, vector<tuple<int, int>>> Umap;
vector<int> answer;
while (true)
{
cin >> NodeSize >> NodeLoadSize;
if (NodeSize == 0 && NodeLoadSize == 0)
break;
cin >> Start >> end;
Umap.clear();
for (int i = 0; i < NodeLoadSize; i++)
{
cin >> node >> Xnode >> Dis;
Umap[node].emplace_back(make_tuple(Dis, Xnode));
}
find_FIRST_DS(Umap, Start, end, NodeSize);
answer.emplace_back(find_second_DS(Umap, Start, end, NodeSize));
}
for (const auto& an : answer) {
printf("%d\n", an);
}
return 0;
}
'알고리즘' 카테고리의 다른 글
| 알고리즘 [flood fill] (0) | 2024.11.12 |
|---|---|
| 영우의 기숙사 청소 [백준 : 15806번] (0) | 2024.11.05 |
| 부분합 알고리즘 (0) | 2024.10.29 |
| 타잔(Tarjan) 알고리즘 (0) | 2024.07.20 |
| 위상정렬 알고리즘 (1) | 2024.03.29 |