https://www.acmicpc.net/problem/3197

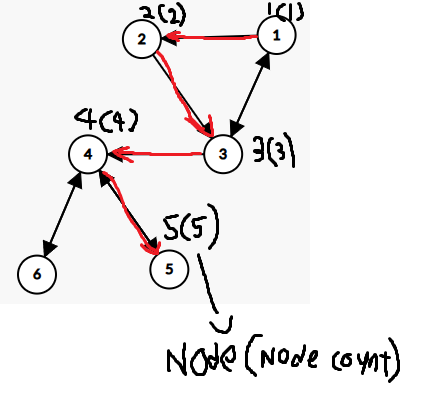
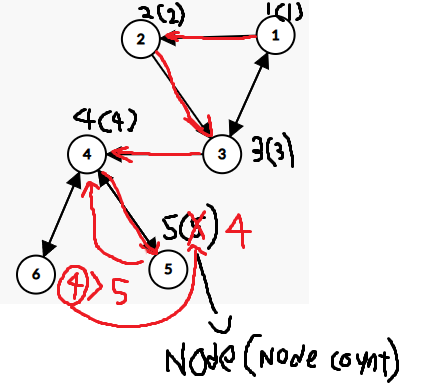
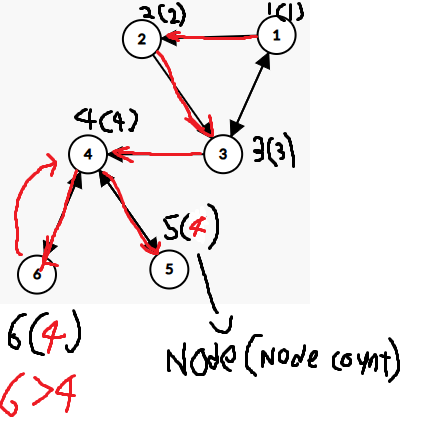
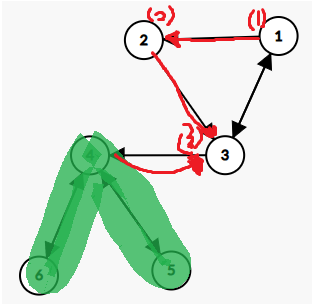
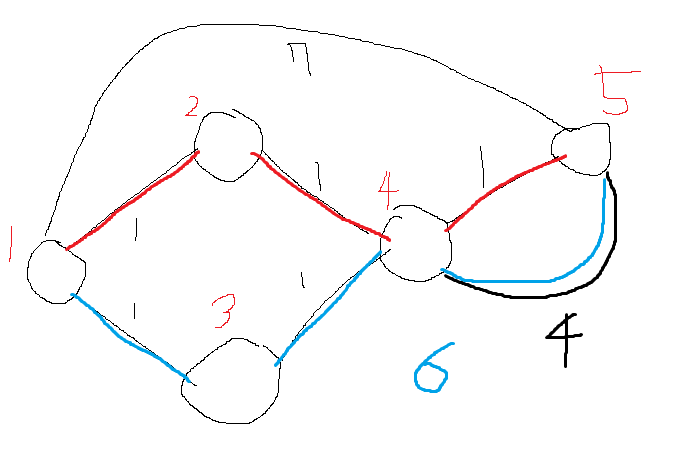
위 이미지처럼
X = 얼음
. = 호수
L = 백조
하루마다 호수에 맞닿아 있는 얼음이 녹는다.
백조는 며칠뒤에 서로 만날 수 있을지 구하는 문제이다.
여기 주소에서 데이터를 받아볼수있다.

문제 풀이에 사용한 알고리즘은
BFS , UnionFind 두개다
문제는 아래 두가지 라고 생각했다.
1.얼음을 녹일 방법
2.백조가 만날수 있는지 확인할수 있는 방법
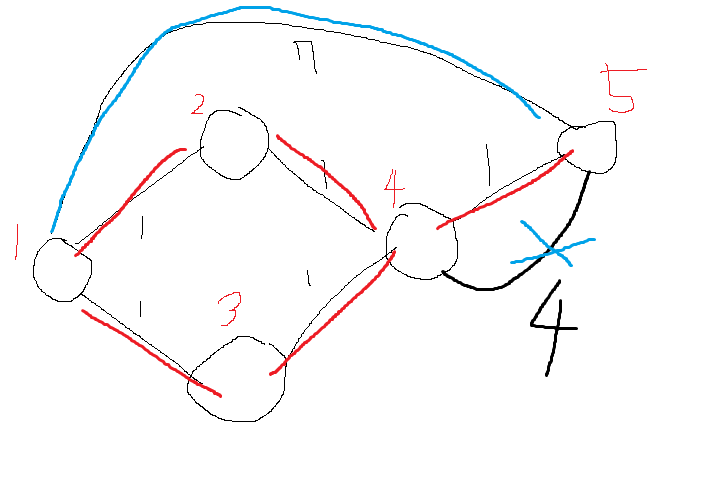
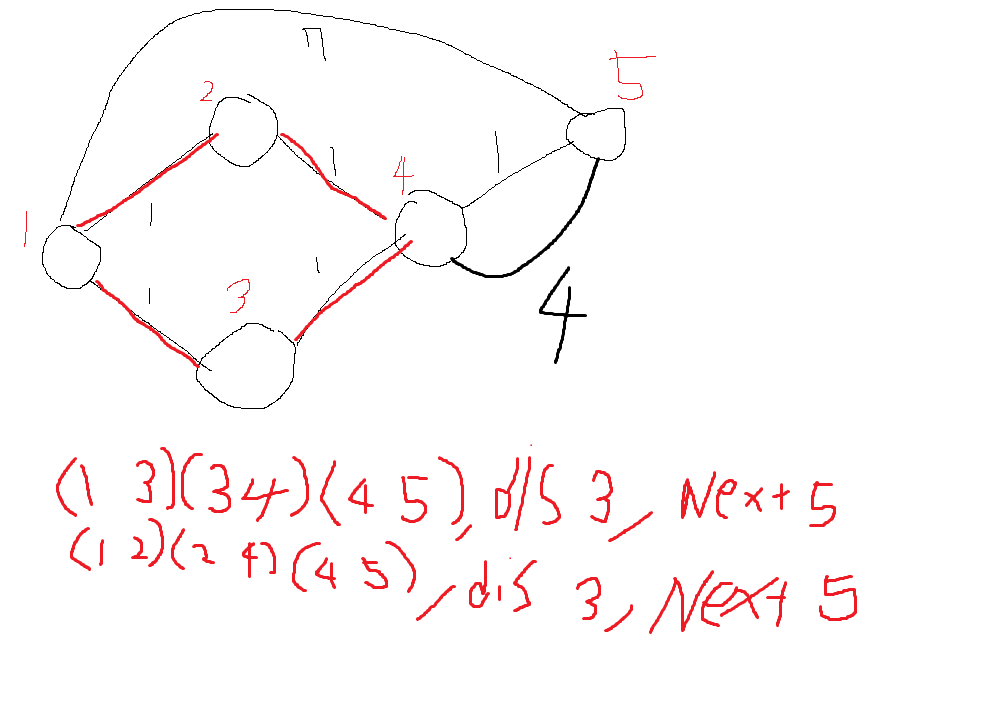
해결방식
1.얼음의 외각을 녹일때 다음 녹을 얼음을 지정해 큐에 넣어준다.
2.얼음마다 지역을 설정해둔뒤 다른지역과 합쳐질때 서로 합쳐준다.
코드
#include<iostream>
#include <queue>
using namespace std;
vector<pair< int, int>> Swans;
queue<pair<int, int>> X_queue, TempQueue, * PointerQueue, * TempPointerQueue;
const static vector < vector<int>> Mover{ {1,0},{0,1},{-1,0},{0,-1} };
const static vector < vector<int>> InputMover{ {0,-1},{-1,0} };
vector<int> lakeList;
int UnionFInd(int Num) {
if (lakeList[Num] == Num)
return Num;
return lakeList[Num] = UnionFInd(lakeList[Num]);
}
void Union(int Left, int Right) {
int LNum = UnionFInd(Left);
int RNum = UnionFInd(Right);
if (LNum == RNum)return;
if (LNum > RNum) {
lakeList[LNum] = RNum;
}
else {
lakeList[RNum] = LNum;
}
}
enum Tile
{
X = -88,
x = -120,
L = -76,
dot = -46
};
void SwanLake() {
int R, C;
cin >> R >> C;
vector<vector<int>> lake(R, vector<int>(C));
vector< int> L_Point(2);
int numb = 1;
lakeList.push_back(0);
for (int i = 0; i < R; ++i) {
for (int j = 0; j < C; ++j) {
char chardata;
cin >> chardata;
lake[i][j] = -(int)chardata;
if (chardata == 'L') Swans.push_back({ i,j });
int after = -1, before = -1;
for (auto M : InputMover) {
if (0 > i + M[0] || 0 > j + M[1] || R <= i + M[0] || C <= j + M[1])continue;
if ((lake[i][j] == Tile::dot || lake[i][j] == Tile::L) && lake[i + M[0]][j + M[1]] == Tile::X) {
X_queue.push({ i + M[0],j + M[1] });
lake[i + M[0]][j + M[1]] = Tile::x;
}
if (lake[i][j] == Tile::X && lake[i + M[0]][j + M[1]] > 0) {
X_queue.push({ i,j });
lake[i][j] = Tile::x;
}
if ((lake[i][j] == Tile::dot || lake[i][j] == Tile::L) && lake[i + M[0]][j + M[1]] > 0) {
if (after == -1) {
after = lake[i + M[0]][j + M[1]];
}
else {
before = lake[i + M[0]][j + M[1]];
}
}
}
if ((lake[i][j] == Tile::dot || lake[i][j] == Tile::L)) {
if (after == -1) {
lake[i][j] = numb;
lakeList.push_back(numb++);
}
else if (before == -1) {
lake[i][j] = after;
}
else {
Union(after, before);
lake[i][j] = UnionFInd(after);
}
}
}
}
for (int i = 0; i < 2; ++i) {
L_Point[i] = (lake[Swans[i].first][Swans[i].second]);
}
int day = 0;
if (UnionFInd(L_Point[0]) == UnionFInd(L_Point[1])) {
cout << day;
return;
}
do {
day++;
PointerQueue = &((X_queue.empty()) ? TempQueue : X_queue);
TempPointerQueue = &((!X_queue.empty()) ? TempQueue : X_queue);
while (!PointerQueue->empty())
{
auto data = PointerQueue->front();
PointerQueue->pop();
int Isbridge = 0;
int firstbridge = -1, secondbridge = -1;
for (auto M : Mover) {
if (0 > data.first + M[0] || 0 > data.second + M[1] || R <= data.first + M[0] || C <= data.second + M[1])continue;
if (lake[data.first + M[0]][data.second + M[1]] == Tile::X)
{
lake[data.first + M[0]][data.second + M[1]] = Tile::x;
TempPointerQueue->push({ data.first + M[0] ,data.second + M[1] });
}
else if (lake[data.first + M[0]][data.second + M[1]] >= 0) {
if (Isbridge != 0) {
Union(lake[data.first][data.second], lake[data.first + M[0]][data.second + M[1]]);
}
else {
Isbridge = lake[data.first + M[0]][data.second + M[1]];
lake[data.first][data.second] = Isbridge;
}
}
}
}
if (UnionFInd(L_Point[0]) == UnionFInd(L_Point[1]))break;
} while (!TempPointerQueue->empty());
cout << day;
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(0);
std::cout.tie(0);
SwanLake();
}
'알고리즘' 카테고리의 다른 글
| 전력난 [백준:6497] 골드 (3) | 2024.11.14 |
|---|---|
| 알고리즘 [flood fill] (0) | 2024.11.12 |
| 영우의 기숙사 청소 [백준 : 15806번] (0) | 2024.11.05 |
| 부분합 알고리즘 (0) | 2024.10.29 |
| 타잔(Tarjan) 알고리즘 (0) | 2024.07.20 |